A^2-Nets: Double Attention Networks

在这篇论文中作者基于 self-attention 机制和 SENet 的启发，提出了double attention 机制。其核心思想是首先将整个空间的关键特征收集到一个紧凑的集合中，然后自适应地将它们分配到每个位置，以便后续的卷积层即使没有大的感受野可以感知整个空间的特征。

论文链接

Method

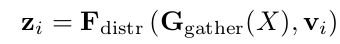
第一个 attention 操作称之为 gather， $G_{gather}$ 是计算整个输入特征 X 的二阶池化(不同于 SENet 中的 global average pooling)，第二个 attention 操作称之为 distribute， $F_{distr}$ 把 $G_{gather}$ 捕捉到的特征应用到每一个 location i 的特征向量 $v_i$ 上。

1. The First Attention Step: Feature Gathering

   给定两个输入特征图 A 和 B，bilinear pooling 定义如下：

   

   

   

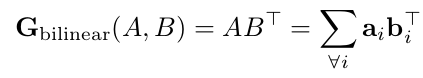
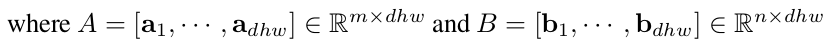
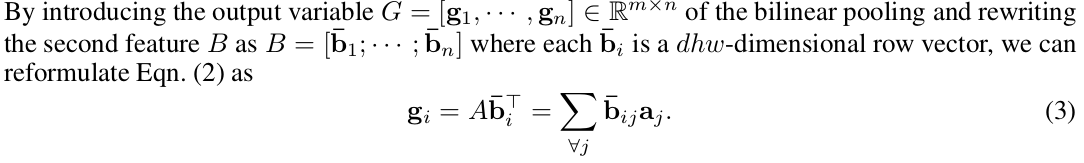
   每一个 $g_i$ 是特征 A 乘上权重 $\overline{b_i}^T$ 得到的结果， 因此我们把 softmax 应用到 B，然后再与 A 相乘：

   

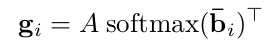
2. The Second Attention Step: Feature Distribution

   

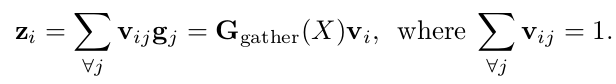
   这里 $v_i$ 也是每个位置特征向量经过 softmax 函数计算的结果。

3. The Double Attention Block

   最后整个 double attention operation 的公式如下：

   

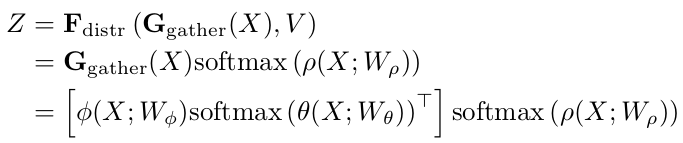
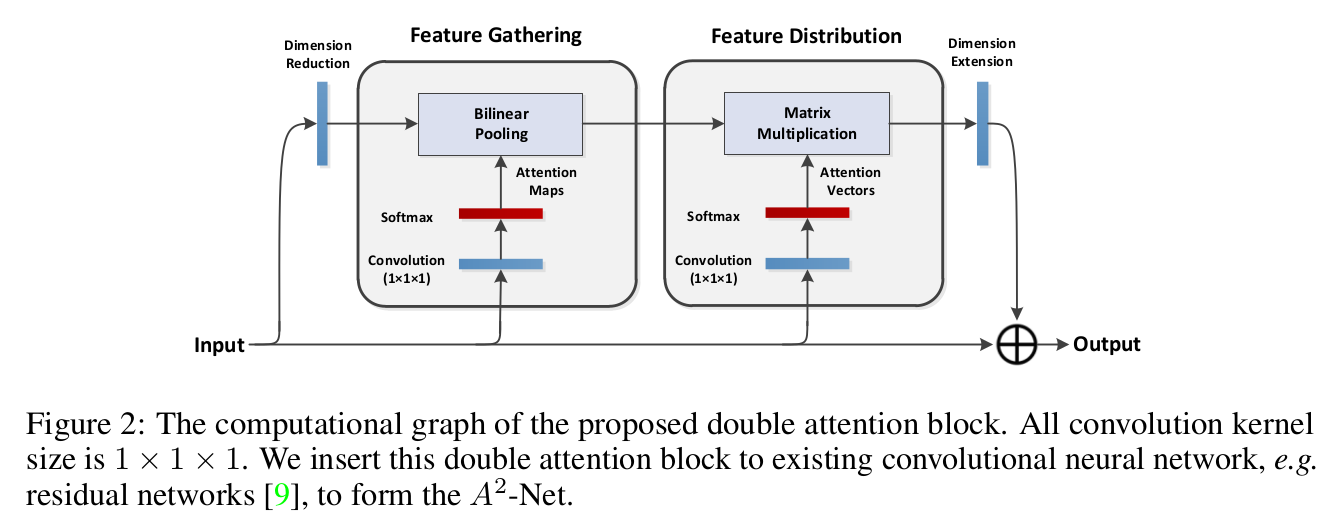
   double attention 操作过程如下图所示：

   

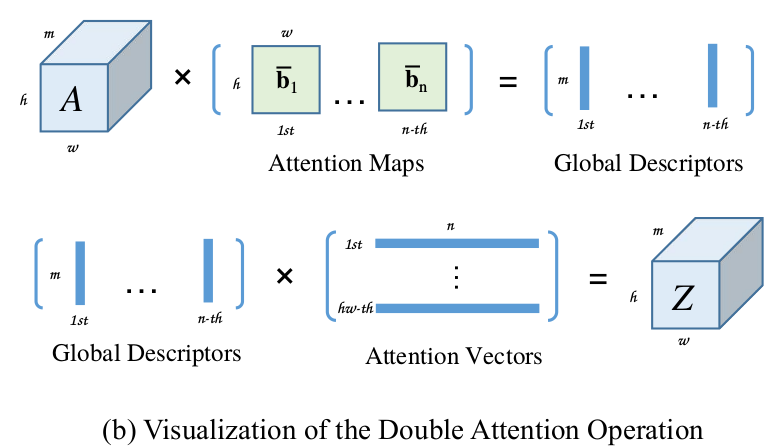
   图中上面一行是第一个 attention operation：m×hw 维特征与 hw×n 维特征得到 m×n 维，下面一行是第二个 attention operation：m×n 维特征与 n×hw 维得到最后的 m×h×w 维输出。

   整个 double attention block 如下图所示，在两步 attention 之后加入了残差结构：

   

4. 与 non-local operation 比较

   根据乘法结合律，double attention 的公式可以先计算右边：

   

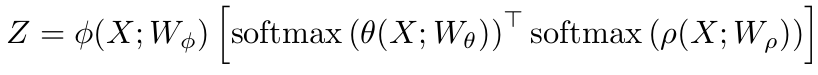
   这样计算过程其实与 non-local operation 一样，先是 hw×n 维特征与 n×hw 维得到 hw×hw，然后 m×hw 维特征再与这 hw×hw 的特征得到 m×h×w 维输出。

   但是，先计算左边的复杂度为O(mndhw)，而先计算右边的复杂度为 $O(m(dhw)^2)$ ，所以本文利用乘法结合率，大大降低了 non-local operation 或者说 self-attention 的计算量，本质上与non-local operation没有任何区别，而在使用结合律的时候加入 softmax 进行归一化可以理解为对于某一维度进行了近似表示，再根据这组近似表示去更新context(参考)。

---

• Previous
  Non-local Neural Network
• Next
  线性SVM

---