Non-local Neural Network

在深度神经网络中捕捉长距离依赖(long-range dependencies)是非常重要的，对于图片数据，传统的方法是通过堆叠卷积操作扩大感受野来获得长距离依赖。作者在这篇论文中受计算机视觉中传统的 non-local means 方法的启发，提出了 non-local operation 来捕捉长距离依赖。

论文链接

传统的卷积是在局部领域内进行操作，堆叠卷积有几点限制：

1. 计算效率低下
2. 网络优化困难
3. 远距离信息传播困难

Formulation

通用的 Non-local operation 定义如下：

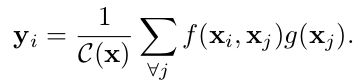
i 是一个当前要计算的位置(在空间、时间或者时空维度)，j 是所有其他可能的位置，x 是输入信号，一般是特征，y 是与x具有相同size的输出特征，函数 f 计算位置 i 与所有位置 j 之间相似性关系，一元函数 g 计算出所有位置 j 的输入信号的一种表征，C(x) 用来对输出进行正则化。

Instantiations

对于函数g，简单地把 g 考虑成线性操作： $g(x_j)=W_gx_j$

在神经网络中 g 用1×1(空间维度)或者1×1×1(时空维度)的卷积来实现。

对于函数f，有不同的选择：

• Gaussian

$$f(x_i,x_j)=e^{x_i^Tx_j}$$ $$C(x)=sum_{\forall j}f(x_i,x_j)$$

• Embedded Gaussian

$$f(x_i,x_j)=e^{ {\theta}(x_i)^T{\phi}(x_j)}$$ $${\theta}(x_i)=W_{\theta}x_i$$ $${\phi}(x_j)=W_{\phi}x_j$$ $$C(x)=sum_{\forall j}f(x_i,x_j)$$

   self-attention 机制就是 Non-local Operation 的 Embedded Gaussian 版，对于给定 i， $\frac{1}{C(x)}f(x_i,x_j)$ ​ 就是计算所有 j 的 softmax 函数，所以我们有 $y=softmax(x^TW_{\theta}^TW_{\phi}x)g(x)$

• Dot product

$$f(x_i,x_j)={\theta}(x_i)^T{\phi}(x_j)$$ $$C(x)=N$$

• Concatenation

$$f(x_i,x_j)=ReLU(w_f^T[{\theta}(x_i)^T,{\phi}(x_j)])$$

​   这里 $[\cdot,\cdot]$ ​ 表示 concatenation，

$$C(x)=N$$

Non-local Block

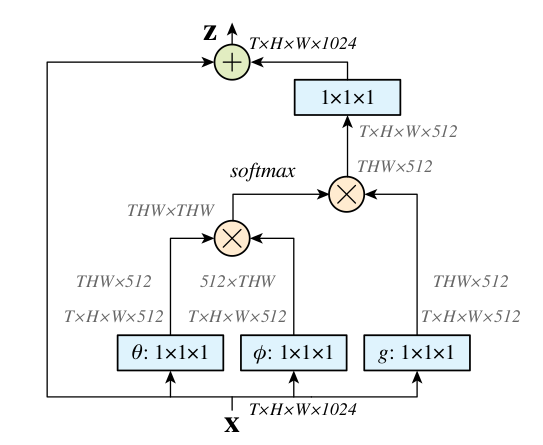
输入维度 T×H×W×1024，经过 1×1×1 的卷积 $\theta$ 和 $\phi$ 后得到两个 T×H×W×512 维的特征(这里通道数减半可以减少计算量)，分别 reshape 成 THW×512 和 512×THW，再进行矩阵相乘得到 THW×THW 维的矩阵，再经过 softmax 得到每个点对应一个 THW 维的权重向量，表示所有 T×H×W 个点与该点之间的关系，可以说每个点都捕捉到了全局的特征。然后 softmax 的输出再与 g 的输出相乘。

最后使用残差结构 $z_i = W_zy_i+x_i$ 使得我们可以把 non-local block 插入到任何已有的预训练模型中。

Visualization

把 softmax 计算出的维度为 THW×THW 的结果中某一个点的 1×THW 的权重向量中值最大的几个点可视化出来：

---

• Next
  A^2-Nets: Double Attention Networks

---